Ikubaru's Blogzia-Baris dan deret banyak digunakan dalam kehidupan sehari-hari, misalnya dalam mengukur kecepatan kendaraan pada speedometer. Dalam speedometer terdapat angka-angka yang memiliki pola tertentu sehingga membentuk sebuah barisan aritmatika.
Dalam Ilmu Ekonomi baris dan deret banyak digunakan dalam hal menghitung pertumbuhan penduduk dan pangan, mengukur biaya produksi dan pendapatan, serta menghitung bunga majemuk dalam dunia perbankan.
DASAR-DASAR BARIS DAN DERET
- Barisan Aritmatika (Hitung)
Barisan Aritmatika (Hitung) ialah barisan yang perubahan suku-sukunya mempunyai selisih atau perbedaan (b) yang sama. Barisan aritmatika diperoleh dengan menjumlahkan bilangan tertentu ke bilangan sebelumnya untuk mendapatkan suku berikutnya. Bentuk umum suku ke-n dalam barisan aritmatika ialah:
Dimana : Un = Suku ke n
a = Suku pertama
b = Beda atau selisih
n = Banyaknya suku
- Deret Aritmatika (Hitung)
Deret Aritmatika (Hitung) ialah penjumlahan dari suku-suku suatu barisan aritmatika. Bentuk umum jumlah n suku pertama deret aritmatika ialah:
Dimana : Sn = Suku ke n
a = Suku pertama
b = Beda atau selisih
n = Banyaknya suku
- Barisan Geometri (Ukur)
Barisan Geometri (Ukur) ialah barisan bilangan dengan perbandingan setiap suku dengan suku sebelumnya selalu sama. Perbandingan setiap suku berurutannya disebut rasio (r). Bentuk umum dari Barisan Geometri (Ukur) ialah:
- Deret Geometri (Ukur)
Deret Geometri (Ukur) ialah penjumlahan dari suku-suku suatu barisan geometri (Ukur). Bentuk umum dari Deret Geometri (Ukur) ialah:
Dimana : Un = Suku ke n
a = Suku pertama
r = rasio
n = Banyaknya suku
APLIKASI DALAM ILMU EKONOMI BISNIS
- Deret dalam Mengukur Pertumbuhan Penduduk
Menurut Robert Malthus, dalam mengukur Pertumbuhan Penduduk mengikuti Barisan Geometri (Ukur), sedangkan Pertumbuhan Pangan mengikuti Barisan Aritmatika (Hitung).
Secara Matematis dapat dirumuskan:
Dimana : Pt = Jumlah penduduk pada periode t
Pi = Jumlah penduduk pada awal periode
r = pertumbuhan penduduk (%)
t = Selisih waktu pada awal periode hingga periode t
Di Kota A pada tahun 2000 jumlah penduduknya sebnayak 2.000.000 jiwa dab menurut historis perhitungan tingkat pertumbuhan penduduknya sebesar 2% / tahun. Berapa jumlah penduduk di Kota A tahun 2004?
- Barisan dalam Usaha Bisnis
Penerapan barisan bagi dunia bisnis yang lebih sesuai adalah Barisan Aritmatika. Karena apabila diukur dengan barisan geometri, variabel-variabel ekonomi seperti biaya produksi, modal, pendapatan, tenaga kerja akan kesulitan untuk mengikutinya dalam arti segera memenuhinya.
Contoh: Stok barang PT. X pada bulan 1 sampai dengan 10, setelah dihitung rata-rata permintaan barang tersebut ialah 7. Berapakah stok barang pada bulan ke-6
- Deret dalam Mengukur Bunga Majemuk
Model deret untuk bunga majemuk (Bunga berbunga) ialah baris geometri khususnya bagi hutang piutang. Hal ini berlaku bagi dunia perbankan. Transaksi dengan model ini disebut kredit.
Rumus:
Rumus ini untuk kredit system pembayaran suku bunga yang dibayarkan setahun sekali. Sebaiknya jika suku bunga dibayarkan lebih dari satu kali dalam setahun rumusnya menjadi:
Contoh :
Mr. Bean kredit mobil dengan uang muka 10.000.000, sisa kreditnya yaitu 30.000.000 dengan suku bunga kredit 2% / bulan dalam jangka waktu 2 tahun. Berapakah jumlah kredit setelah jatuh tempo pelunasan dan berapakah jumlah harga mobil?
Referensi:
Anwar, Cecep, dkk. 2008. Matematika Aplikasi.
Sunyoto, Danang. 2011. Matematika Ekonomi dan Bisnis.
Sulistiyono. 2007. SPM Matematika.
Anwar, Cecep, dkk. 2008. Matematika Aplikasi.
Sunyoto, Danang. 2011. Matematika Ekonomi dan Bisnis.
Sulistiyono. 2007. SPM Matematika.
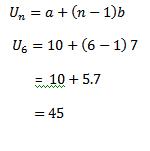
Sangat memusingkan bila harus berjibaku dengan persamaan-persamaan deret
ReplyDeleteuntuk nilai sekarang dan bunga pinjaman??
ReplyDeleteIzin koreksi, mohon maaf sblmny Ad yg kurang pada rumus SN
ReplyDeleterumus untuk bunga majemuk, hubungan antara P dan ( 1+ ....) bukan + tapi X. Makasih....
ReplyDeleteJika diketahui a:100 dan S7:160 yg ditanyakan beda (b) bgmana rumus nya pak?trmksh
ReplyDelete